Floarea vieţii şi Solidele Platon ( 1 )
( construcţie geometrică )

Construcţie :
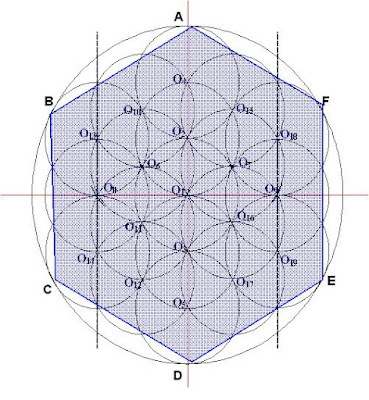
– desenăm cercul de centru O1 şi rază R ( lungimea razei – după necesităţi ) este numit cercul de lucru, întreaga compoziţie are ca părţi numai astfel de de cercuri ; punctul O1 este şi centrul sistemului de axe rectangulare în planul de lucru.
– pe axa verticală de la cercul – origine în sus constuim două cercuri cu centrele în O2 şi O4 care determină două Vezica Piscis – mari cu axele lor mari pe orizontală şi de la origine în jos alte două cercuri cu centrele în O3 şi O5. Cu centrul în O1 şi de rază cât trei raze ale cercului de lucru construim cercul cuprinzător care va fi tangent cercurilor cu centrele în O4 şi O5. Punem în evidenţă capetele axei mari ale unei Vezica Piscis, de exemplu O6 şi O7.
– cercul cu centrul în O6 intersectează axa orizontală în O8 , iar cercul cu centrul în O7 intersectează axa orizontală în O9.
– construim cercurile cu centrele în O8 şi O9 şi verticalele în aceste puncte, iar cu centrele pe aceste două verticale construim şi cercurile cu centrele în O13,O14,O18,O19 .
– construim „ cercurile pline “ cu centrele în : O10,O6 , O11 , O12 , O13 , O7 , O16 , O17,. A fost posibil să construim 19 cercuri pline.

– construim dreptele - suport care trec prin punctele A-F, B-E,C-D , O4-O18,
O10-O9,O8O17, O14-O5 şi dreptele - suport care trec prin punctele A - B,C -F,
D-E ,O4-O13 , O8 - O13 , O8 - O15 , O9-O12 , O5-O19. Aceste oblice se intersectează în afara cercului cuprinzător în una din variantele: oblică - oblică, oblică – verticală sau oblică – orizontală şi sunt determinate punctele P1 , P2 ... P18 , centrele unor cercuri de lucru din care vom folosi numai arce - a şasea parte dintr-un astfel de cerc.
– Celula de Apă se multiplică la nesfârşit în această reţea, Floarea Vieţi este o delimitare prin convenţie din această reţea, delimitare care nu afost făcută întâmplător: proiecţiile în D2 ale Solidelor Platon se regăsesc în această structură.
– în dialogul Timaios filozoful defineşte partea cea mai simplă care stă la originea celor patru corpuri elementare:
„ Vom începe cu figura cea mai simplă şi cea mai mică; elementul ei este triunghiul care are ipotenuza de două ori mai lungă decât latura cea mai scurtă “
„ Cât despre noi, lăsându-le la o parte pe toate celelalte, postulăm că dintre aceste triunghiuri unul este cel mai frumos : acela din care o pereche formează un al treilea triunghi, cel echilateral. “
– triunghi Platon , „ cel mai frumos “ : O1KO7 şi echilateral : O1O17O7.
– Celula de apă este acoperită de 12 triunghiuri Platon.

– constuim cercuri cu centrele în Q1, Q2 , Q3 , O4 , ... , Q12 , însă pentru desenul în D2 la Floarea vieţii folosim din ele numai semicercuri.
– constuim cercuri cu centrele în A, B, … F, însă pentru desenul în D2 la Floarea vieţii folosim din ele numai treimi .

– Platon : „ Iar acum trebuie să arătăm ce anume proprietăţi ar fi să aibă corpurile cele mai frumoase pentru a fi : patru la număr şi diferite unele de altele , însă astfel încât , în timp ce se descompun , să se poată constitui unele din altele. Dar dacă izbutim acest lucru , iată-ne în posesia adevărului cu privire la naşterea pământului şi a focului , precum şi a corpurilor care se situează , proporţional între ele ( apa şi aerul – notă adăugată R. G. !). Căci nu vom admite în faţa nimănui că pot exista corpuri vizibile mai frumoase decât acestea , fiecare corespunzând unui singur tip ( un anume fel de figură în spaţiu - nota 124 – Cătălin Partenie ).
Din : Platon , Opere VII 1993 – Editura Ştiinţifică – Timaios - traducere şi note – Cătălin Partenie .
– în prezent suntem suprasaturaţi de modelul unui atom: nişte biluţe,fie îngrămădite în nucleu, fie fără odihnă alergând pe orbite. Particulele cele mai mici ale lui Platon sunt „ triunghiurile frumoase“; cât de mici ? Aici a funcţionat <> : atât de mici încât cu mintea nu le putem imagina, adică , la nevoie , avem libertatea să depăşim ultimul prag. Alegerea triunghiului ( cel mai simplu poligon „care cuprinde“, delimitează o parte din D2) nu-i întâmplătoare : corespondenţa ce se doreşte a fi determinată între elementele primordiale şi Solide face apel , până la urmă, la acest poligon; proiecţiile Solidelor în D2 sunt asamblate după linii din Floarea vieţii – la rândul ei compusă numai din triunghiuri frumoase.

– în reţeaua fără sfârşit din care provine Floarea vieţii, Celula de Apă – unitate de lucru în dualitate virtuală cu cercul de lucru, se repetă , evident , fără sfârşit; o Celulă de Apă include 12 triunghiuri Platon.
– punctele P1, P2, … P18 , zte trei sunt coliniare, fiind determinate şase derepte, care intersectându-se două câte două , la rândul lor , determină o Celulă de Apă.
– notă: afirmaţiile din această postare , chair cele compuse cu ocazia construcţiei la Floarea vieţii nu au primit justificări , acestea fiind exerciţii
simple de geometrie plană; construcţia „ ştiinţifică “ trebuie să respecte regulile clasice folosite la construcţiile cu rigla şi compasul. Este posibil să observăm , chiar şi din această postare că trebuie să plecăm de undeva, să avem o unitate de lucru, să respectăm ( totuşi !) anumite convenţii care au devenit stabile în timp . Natura dublă a domeniului : geometrie + sacralitate ne obligă să luăm aminte !

– cercurile cu centrele în O4, O13, O14 , O5 , O19 şi O18 sunt tangente cercului ce are lungimea razei de trei ori cât lungimea cercului de lucru – în punctele A, B, C, D, E şi F , puncte care sunt vârfurile Celulei de Apă.


Bibliografie
1. http://rozetaalbastra.blogspot.com/
2. http://vremuialavremii.blogspot.com/
3. http://picasaweb.google.com/rot.grigore
4. http://www.crestinortodox.ro/credinta/sinoadele-ecumenice-bisericii-69801.html
5. http://vismitsimbol.blogspot.com/2009/02/sanzienele.html
6. Traian Lalescu - Geometria triunghiului, Editura Apollo, Craiova 1993
8. Ion Pascaru, Petre Nachila - Matematica gimnaziala in concursurile scolare,
Editura Tiparg 2005
9 Ion Chitescu, Marcel Chirita – Geometria patrulaterului, Editura Teora, 1998
12. Constantin Ionescu – Tiu - Geometrie plana si in spatiu pentru admitere,
Editura Albatros 1976
13. http://www.jesus8880.com/chapters/gematria/vesica-pisces.htm
15. Liviu Nicolescu, Vladimir Broskov – Probleme practice de geometrie, Editura Tehnica Bucuresti 1990
16. http://translate.google.ro/translate?hl=ro&sl=en&u=http://www.brucerawles.
17. Miron Oprea – Scurta istorie a matematicii, Editura Premier, Ploiesti 2000
18. Platon – Opere VII – Editura ştiinţifică , Bucureşti 1993.
de Rotaru Grigore Delacamboru